
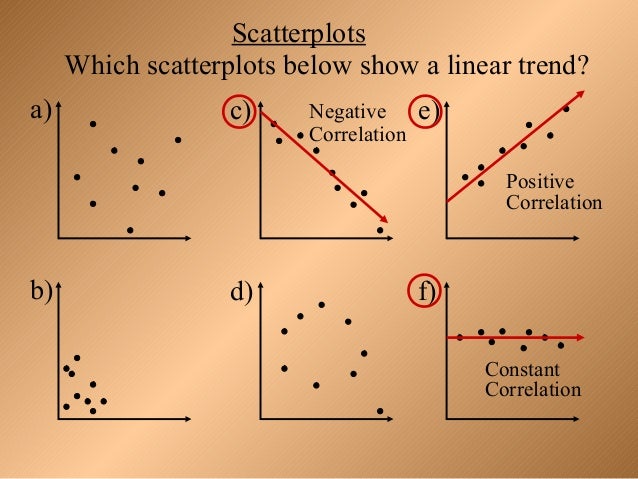
When you look at a scatterplot, you want to notice the overall pattern and any deviations from the pattern. Consider a scatter plot where all the points fall on a horizontal line providing a "perfect fit." The horizontal line would in fact show no relationship. For a linear relationship there is an exception. You can determine the strength of the relationship by looking at the scatter plot and seeing how close the points are to a line, a power function, an exponential function, High values of one variable occurring with low values of the other variable.High values of one variable occurring with high values of the other variable or low values of one variable occurring with low values of the other variable.A clear direction happens when there is either: This variable served as the investigator's measure of the individual's intelligence.Construct a scatter plot and state if what Amelia thinks appears to be true.Ī scatter plot shows the direction of a relationship between the variables. Response ( y): Performance IQ scores ( PIQ) from the revised Wechsler Adult Intelligence Scale.Interested in answering the above research question, some researchers (Willerman, et al, 1991) collected the following data ( IQ Size data) on a sample of n = 38 college students: Are a person's brain size and body size predictive of his or her intelligence? For now, my hope is that these examples leave you with an appreciation of the richness of multiple regression. In the upcoming lessons, we will revisit similar examples in greater detail. Most of all, don't worry about mastering all of the details now. You might also try to pay attention to the similarities and differences among the examples and their resulting models. Make sure you notice, in each case, that the model has more than one predictor. Let's jump in and take a look at some "real-life" examples in which a multiple linear regression model is used. With a minor generalization of the degrees of freedom, we use prediction intervals for predicting an individual response and confidence intervals for estimating the mean response.With a minor generalization of the degrees of freedom, we use t-tests and t-intervals for the regression slope coefficients to assess whether a predictor is significantly linearly related to the response, after controlling for the effects of all the other predictors in the model.However, with multiple linear regression, we can also make use of an "adjusted" \(R^2\) value, which is useful for model-building purposes. We'll explore this measure further in Lesson 10. The use and interpretation of \(R^2\) in the context of multiple linear regression remains the same.We'll explore this issue further in Lesson 7. All of the model-checking procedures we learned earlier are useful in the multiple linear regression framework, although the process becomes more involved since we now have multiple predictors. The only real difference is that whereas in simple linear regression we think of the distribution of errors at a fixed value of the single predictor, with multiple linear regression we have to think of the distribution of errors at a fixed set of values for all the predictors. The models have similar "LINE" assumptions.Think about it - you don't have to forget all of that good stuff you learned! In particular: The good news is that everything you learned about the simple linear regression model extends - with at most minor modifications - to the multiple linear regression model. If you're unsure about any of this, it may be a good time to take a look at this Matrix Algebra Review. This lesson considers some of the more important multiple regression formulas in matrix form. In the multiple regression setting, because of the potentially large number of predictors, it is more efficient to use matrices to define the regression model and the subsequent analyses. That is, we use the adjective "simple" to denote that our model has only predictors, and we use the adjective "multiple" to indicate that our model has at least two predictors. We move from the simple linear regression model with one predictor to the multiple linear regression model with two or more predictors. In this lesson, we make our first (and last?!) major jump in the course.


 0 kommentar(er)
0 kommentar(er)
